基础

1. 二分查找

function binarySearch(nums: number[], target: number): number {
    let left = 0,
        right = nums.length - 1;
    while (left <= right) {
        const mid = (left + right) >> 1;
        if (nums[mid] > target) right = mid - 1;
        else if (nums[mid] < target) left = mid + 1;
        else return mid;
    }
    return -1;
}

1.有序数组元素可能重复，查找第一个出现的元素

function searchFirst(nums: number[], target: number): number {
    let left = 0,
        right = nums.length - 1;
    while (left < right) {
        const mid = (left + right) >> 1;
        if (nums[mid] < target) left = mid + 1;
        else if (nums[mid] === target) right = mid;
        else right = mid - 1;
    }
    return nums[left] === target ? left : -1;
}

2.有序数组元素可能重复，查找最后一个出现的元素

function searchLast(nums: number[], target: number): number {
    let left = 0,
        right = nums.length - 1;
    while (left < right) {
        const mid = (left + right + 1) >> 1;
        if (nums[mid] < target) left = mid + 1;
        else if (nums[mid] === target) left = mid;
        else right = mid - 1;
    }
    return nums[left] === target ? left : -1;
}

2. 十六进制转 RGB

String.prototype.hexToRgb = function () {
    let sColor = this.toLowerCase();
    const reg = /^#([0-9a-fA-F]{3}|[0-9a-fA-F]{6})$/;
    if (sColor && reg.test(sColor)) {
        // 3位转6位
        if (sColor.length === 4) {
            let sColorNew = '#';
            for (let i = 1; i < 4; i++) {
                sColorNew += sColor.charAt(i).repeat(2);
            }
            sColor = sColorNew;
        }
        // 十六进制转RGB
        const sColorRange = [];
        for (let i = 1; i < 7; i += 2) {
            sColorRange.push(parseInt(sColor.slice(i, i + 2), 16));
        }
        return 'rgb(' + sColorRange.join(', ') + ')';
    }
    return sColor;
};

3. 树的遍历

以下以二叉树为例

1.深度优先遍历

定义：对每一个可能的分支路径深入到不能再深入为止，而且每个结点只能访问一次。深度优先遍历又分为：

• 先序遍历：对任一子树，先访问根，然后遍历其左子树，最后遍历其右子树
• 中序遍历：对任一子树，先遍历其左子树，然后访问根，最后遍历其右子树
• 后续遍历：对任一子树，先遍历其左子树，然后遍历其右子树，最后访问根

2.广度优先遍历

又叫层次遍历，从上往下对每一层依次访问，在每一层中，从左往右（也可以从右往左）访问结点，访问完一层就进入下一层，直到没有结点可以访问为止

二叉树的深度优先遍历的非递归的通用做法是采用栈，广度优先遍历的非递归的通用做法是采用队列

3.深度优先搜索算法

不全部保留结点，占用空间少；有回溯操作(即有入栈、出栈操作)，运行速度慢

通常深度优先搜索法不全部保留结点，扩展完的结点从数据库中弹出删去，这样，一般在数据库中存储的结点数就是深度值，因此它占用空间较少。所以，当搜索树的结点较多，用其它方法易产生内存溢出时，深度优先搜索不失为一种有效的求解方法

4.广度优先搜索算法

保留全部结点，占用空间大； 无回溯操作(即无入栈、出栈操作)，运行速度快

广度优先搜索算法，一般需存储产生的所有结点，占用的存储空间要比深度优先搜索大得多，因此，程序设计中，必须考虑溢出和节省内存空间的问题。但广度优先搜索法一般无回溯操作，即入栈和出栈的操作，所以运行速度比深度优先搜索要快些

4. 交换两数

1.添加第三方临时变量

let a = 3,
    b = 5;
const temp = a;
a = b;
b = temp;

2.不使用临时变量（很巧妙）

let a = 3,
    b = 5;
a = a + b;
b = a - b;
a = a - b;

3.采用异或运算特性，安全

let a = 3,
    b = 5;
a = a ^ b;
b = a ^ b;
a = a ^ b;

注意：交换引用类型下同一个数会导致结果变成 0，例如：swap(nums, 0, 0)

4.JS 解构赋值（效率低）

[a, b] = [b, a];

5. 排序

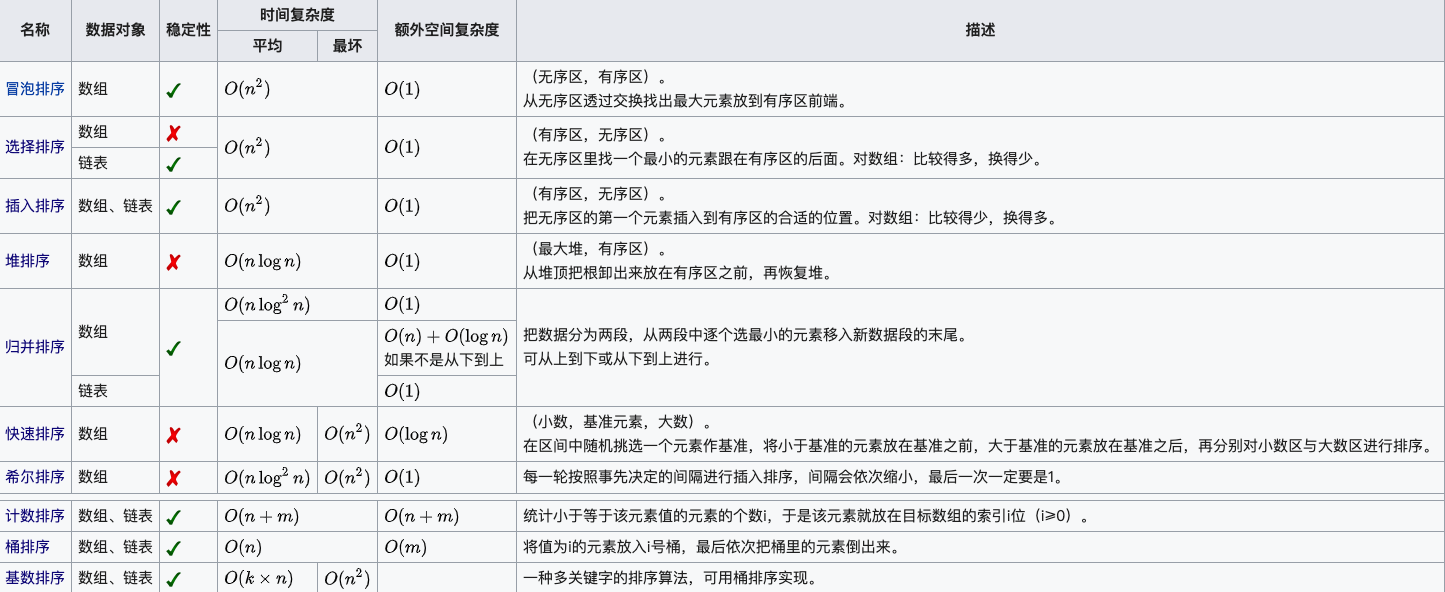
1.冒泡排序

复杂度：时间复杂度 O(n^2^)，空间复杂度 O(1)

核心思想：从前往后，将较大（小）的数往后冒泡，每次确定倒数第 i 位的结果

function bubbleSort(nums: number[]): void {
    const len = nums.length;
    for (let i = 0; i < len - 1; i++) {
        for (let j = 0; j < len - 1 - i; j++) {
            if (nums[j] > nums[j + 1]) {
                nums[j] = nums[j] ^ nums[j + 1];
                nums[j + 1] = nums[j] ^ nums[j + 1];
                nums[j] = nums[j] ^ nums[j + 1];
            }
        }
    }
}

2.选择排序

复杂度：时间复杂度 O(n^2^)，空间复杂度 O(1)

核心思想：从前往后，每次确定开头第 i 位的结果

function selectionSort(nums: number[]): void {
    const len = nums.length;
    let minIdx = 0;
    for (let i = 0; i < len - 1; i++) {
        minIdx = i;
        for (let j = i + 1; j < len; j++) {
            if (nums[j] < nums[minIdx]) minIdx = j;
        }
        if (minIdx !== i) {
            nums[i] = nums[i] ^ nums[minIdx];
            nums[minIdx] = nums[i] ^ nums[minIdx];
            nums[i] = nums[i] ^ nums[minIdx];
        }
    }
}

3.快速排序

参考链接：https://www.runoob.com/w3cnote/quick-sort-2.html

复杂度：时间复杂度 O(n·logn)，空间复杂度 O(logn)

核心思想：从数组中挑出一个元素为基准值（pivot），进行分区操作（partition），递归上述过程

• 分区操作（partition）：将数组使用基准值（pivot）分割

• 基准值左边的元素都小于基准值，右边的元素都大于基准值

function quickSort(nums: number[], left: number, right: number): void {
    if (left < right) {
        const partitionIndex = partition2(nums, left, right);
        quickSort(nums, 0, partitionIndex - 1);
        quickSort(nums, partitionIndex + 1, right);
    }
}

function swap(nums: number[], i: number, j: number): void {
    let temp = nums[i];
    nums[i] = nums[j];
    nums[j] = temp;
}

function partition1(nums: number[], left: number, right: number): number {
    const pivot = nums[left];
    let index = left + 1;
    for (let i = index; i <= right; i++) {
        if (nums[i] < pivot) swap(nums, i, index++);
    }
    swap(nums, left, index - 1);
    return index - 1;
}

function partition2(nums: number[], left: number, right: number): number {
    const pivot = nums[left];
    while (left < right) {
        while (left < right && nums[right] > pivot) right--;
        nums[left] = nums[right];
        while (left < right && nums[left] <= pivot) left++;
        nums[right] = nums[left];
    }
    nums[left] = pivot;
    return left;
}