TOP 100

力扣 top100：https://leetcode-cn.com/problem-list/2cktkvj/

以下编号是 top100 从上往下的编号，并非题目实际的编号

结构声明：

// Definition for singly-linked list.
class ListNode {
    val: number;
    next: ListNode | null;
    constructor(val?: number, next?: ListNode | null) {
        this.val = val === undefined ? 0 : val;
        this.next = next === undefined ? null : next;
    }
}

1. 两数之和

利用 Map 结构（边判断，边存储）

复杂度：时间复杂度 O(n)，空间复杂度 O(n)

function twoSum(nums: number[], target: number): number[] {
    const map: Map<number, number> = new Map();
    for (let i = 0; i < nums.length; i++) {
        const prev = target - nums[i];
        if (map.has(prev)) return [map.get(prev) as number, i];
        else map.set(nums[i], i);
    }
    return [-1, -1];
}

2. 两数相加

直接处理，通过创建默认头结点、已结束列表对应位置值设置为 0，使代码更简洁

复杂度：时间复杂度 O(n)，空间复杂度 O(1)

function addTwoNumbers(l1: ListNode | null, l2: ListNode | null): ListNode | null {
    let curr = new ListNode(),
        carry = 0;
    const head = curr;
    while (l1 || l2 || carry) {
        carry += (l1?.val ?? 0) + (l2?.val ?? 0);
        curr.next = new ListNode(carry % 10);
        curr = curr.next;
        if (l1) l1 = l1.next;
        if (l2) l2 = l2.next;
        carry = Math.trunc(carry / 10);
    }
    return head.next;
}

3. 无重复字符的最长子串长度

滑动窗口，注意左下标位置不能回退，i 必须通过 Math.max()进行判断（案例：'abba'）

function lengthOfLongestSubstring(s: string): number {
    let ans = 0;
    const map: Map<string, number> = new Map();
    for (let l = 0, r = 0; r < s.length; r++) {
        if (map.has(s[r])) l = Math.max(map.get(s[r]) as number, l);
        ans = Math.max(r - l + 1, ans);
    }
    return ans;
}

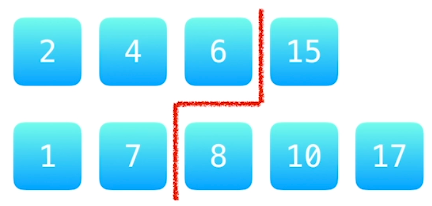
4. 寻找两个有序数组的中位数

思路：二分查找变种、数组分割线

复杂度：时间复杂度 O(log(m+n))，空间复杂度 O(1)

function findMedianSortedArrays(nums1: number[], nums2: number[]): number {
    // 以较短的数组进行二分查找（第一个数组）
    if (nums1.length > nums2.length) return findMedianSortedArrays(nums2, nums1);
    // m、n分别存储nums1、nums2的长度
    const m = nums1.length,
        n = nums2.length;
    // 分割线左边的所有元素需要满足个数 (m + n + 1) / 2（若为奇数则中位数为左侧最大值）
    const totalLeft = Math.floor((m + n + 1) / 2);

    // 在nums1的区间[0, m]中查找恰当的分割线，第二条分割线可根据totalLeft计算位置
    // 分割线需要满足nums1[i - 1] <= nums2[j] && nums[j - 1] <= nums[i]
    // 约定i、j分别位于两个分割线的右边，也等于左侧被分割数组长度
    let left = 0,
        right = m;
    while (left < right) {
        const i = (right + left + 1) >> 1,
            j = totalLeft - i;
        if (nums1[i] < nums2[j - 1]) left = i + 1;
        else right = i;
    }

    const i = left,
        j = totalLeft - i;
    const nums1LeftMax = i === 0 ? Number.MIN_SAFE_INTEGER : nums1[i - 1];
    const nums1RightMin = i === m ? Number.MAX_SAFE_INTEGER : nums1[i];
    const nums2LeftMax = j === 0 ? Number.MIN_SAFE_INTEGER : nums2[j - 1];
    const nums2RightMin = j === n ? Number.MAX_SAFE_INTEGER : nums2[j];

    if ((m + n) % 2 === 1) return Math.max(nums1LeftMax, nums2LeftMax);
    else return (Math.max(nums1LeftMax, nums2LeftMax) + Math.min(nums1RightMin, nums2RightMin)) / 2;
}

5. 最长回文子串

思路一：暴力破解，最长子串为本身、小一个字符子串……进行查找

复杂度：时间复杂度 O(n^3^)，空间复杂度 O(1)

function longestPalindrome(s: string): string {
    // 判断字符串是否是回文字符串
    const palindrome = (s: string): boolean => {
        let l = 0,
            r = s.length - 1;
        while (l < r) {
            if (s[l] !== s[r]) return false;
            l++;
            r--;
        }
        return true;
    };

    let max = s.length;
    while (max > 0) {
        for (let i = 0; i <= s.length - max; i++) {
            const str = s.slice(i, i + max);
            if (palindrome(str)) return str;
        }
        max--;
    }
    return '';
}

思路二：动态规划

1. 状态：dp[i][j]表示子串s[i...j]是否为回文子串
2. 状态转移方程：dp[i][j] = s[i] === s[j] && dp[i + 1][j - 1]
3. 边界条件：j - 1 - (i + 1) + 1 < 2整理得j - i < 3 <==> j - i + 1 < 4（s[i...j]长度为 2 或者 3 时，不用检查子串是否回文）

动态规划其实就是在填写一张表格

复杂度：时间复杂度 O(n^2^)，空间复杂度 O(n^2^)

function longestPalindrome(s: string): string {
    const len = s.length,
        dp: boolean[][] = [];
    for (let i = 0; i < len; i++) {
        dp.push([]);
        dp[i][i] = true;
    }
    let start = 0,
        maxLen = 1;
    for (let j = 1; j < len; j++) {
        for (let i = 0; i < j; i++) {
            if (s[i] === s[j]) {
                if (j - i < 3) dp[i][j] = true;
                else dp[i][j] = dp[i + 1][j - 1];
                if (dp[i][j] && j - i + 1 > maxLen) {
                    maxLen = j - i + 1;
                    start = i;
                }
            } else dp[i][j] = false;
        }
    }
    return s.slice(start, start + maxLen);
}

思路三：中心扩展法，从一个字符两边扩散，判断是否是回文串

复杂度：时间复杂度 O(n^2^)，空间复杂度 O(1)

function longestPalindrome(s: string): string {
    let start = 0,
        maxLen = 1;
    for (let i = 0; i < s.length - 1; i++) {
        const oddLen = expandAroundCenter(s, i, i);
        const evenLen = expandAroundCenter(s, i, i + 1);
        if (Math.max(oddLen, evenLen) > maxLen) {
            maxLen = Math.max(oddLen, evenLen);
            start = i - Math.trunc((maxLen - 1) / 2);
        }
    }
    return s.slice(start, start + maxLen);
}

function expandAroundCenter(s: string, l: number, r: number): number {
    while (l > -1 && r < s.length && s[l] === s[r]) {
        l--;
        r++;
    }
    return r - l - 1;
}

6. 正则表达式匹配

状态转移方程：

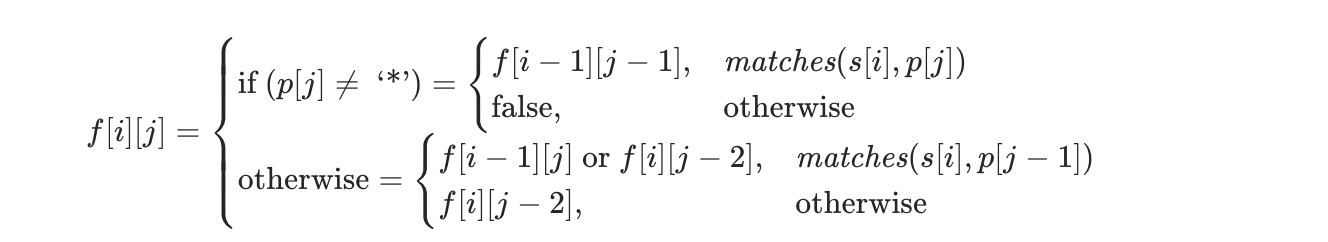
function isMatch(s: string, p: string): boolean {
    const dp = [],
        sLen = s.length,
        pLen = p.length;
    for (let i = 0; i <= sLen; i++) {
        dp.push([]);
    }
    // 初始状态，两个空字符串是匹配的
    dp[0][0] = true;

    // 计算机并不知道输入字符串和匹配传位置会随着移动，需要遍历所有情况，存储状态
    // i，j分别标识第几个字符
    for (let i = 0; i <= sLen; i++) {
        for (let j = 1; j <= pLen; j++) {
            if (p.charAt(j - 1) !== '*') {
                if (matches(s, p, i, j)) dp[i][j] = dp[i - 1][j - 1];
            } else {
                dp[i][j] = dp[i][j - 2];
                if (matches(s, p, i, j - 1)) dp[i][j] = dp[i - 1][j] || dp[i][j];
            }
        }
    }

    return !!dp[sLen][pLen];
}

function matches(s: string, p: string, i: number, j: number): boolean {
    if (i === 0) return false; // 表示终止状态
    if (p.charAt(j - 1) === '.') return true;
    return s.charAt(i - 1) === p.charAt(j - 1);
}

7. 盛最多水的容器

模式识别：需要移动左右两头的问题可以考虑双指针

// 双指针：从两边出发记录面积，每次移动短的一边，一遍过
function maxArea(heights: number[]): number {
    let max = 0,
        left = 0,
        right = heights.length - 1;
    while (left < right) {
        const width = right - left;
        const height = Math.min(heights[left], heights[right]);
        max = Math.max(max, width * height);
        heights[left] < heights[right] ? left++ : right--;
    }
    return max;
}

8. 三数之和

// 排序 + 双指针：固定一个数，剩下两个可通过双指针进行查找
function threeSum(nums: number[]): number[][] {
    nums.sort((a, b) => a - b);
    const res: number[][] = [],
        len = nums.length;
    // 三个数下标分别为i，j，k
    for (let i = 0; i < len; i++) {
        // 枚举的数避免重复操作
        if (i > 0 && nums[i] === nums[i - 1]) continue;
        // 双指针前后遍历，target可为任意元素，此处为0(需要遍历所有结果)
        let k = len - 1,
            target = 0 - nums[i];
        for (let j = i + 1; j < len; j++) {
            if (j > i + 1 && nums[j] === nums[j - 1]) continue;
            while (j < k && nums[j] + nums[k] > target) k--;
            if (j === k) continue;
            if (nums[j] + nums[k] === target) res.push([nums[i], nums[j], nums[k]]);
        }
    }

    return res;
}

另一个版本：

function threeSum(nums: number[]): number[][] {
    nums.sort((a, b) => a - b);
    const res: number[][] = [],
        len = nums.length;
    // 三个数下标分别为i，j，k
    for (let i = 0; i < len - 2; i++) {
        // 枚举的数避免重复操作
        if (i > 0 && nums[i] === nums[i - 1]) continue;
        // 双指针前后遍历(需要遍历所有结果)
        const target = -nums[i];
        let j = i + 1,
            k = len - 1;
        while (j < k) {
            if (j > i + 1 && nums[j] === nums[j - 1]) {
                j++;
                continue;
            }
            if (k < len - 1 && nums[k] === nums[k + 1]) {
                k--;
                continue;
            }
            if (nums[j] + nums[k] > target) k--;
            else if (nums[j] + nums[k] < target) j++;
            else {
                res.push([nums[i], nums[j], nums[k]]);
                j++;
                k--;
            }
        }
    }

    return res;
}

js 数组默认排序方式是按照字符串进行排序的，可传入回调函数按照指定规则排序

[11, 1, 2].sort(); // [1, 11, 2]
[11, 1, 2].sort((a, b) => a - b); // [1, 2, 11]

9. 电话号码的字母组合

回朔算法：

function letterCombinations(digits: string): string[] {
    const combinations: string[] = [];
    if (digits.length === 0) return combinations;

    const keyMap = new Map();
    keyMap.set('2', 'abc');
    keyMap.set('3', 'def');
    keyMap.set('4', 'ghi');
    keyMap.set('5', 'jkl');
    keyMap.set('6', 'mno');
    keyMap.set('7', 'pqrs');
    keyMap.set('8', 'tuv');
    keyMap.set('9', 'wxyz');

    backtrack(digits, combinations, keyMap, 0, []);
    return combinations;
}

function backtrack(
    digits: string,
    combinations: string[],
    keyMap: Map<string, string>,
    index: number,
    buffer: string[]
): void {
    if (index === digits.length) combinations.push(buffer.join(''));
    else {
        const digit = digits.charAt(index);
        const letters = keyMap.get(digit);
        for (let i = 0; i < letters.length; i++) {
            buffer.push(letters.charAt(i));
            backtrack(digits, combinations, keyMap, index + 1, buffer);
            buffer.splice(index, 1);
        }
    }
}

10. 删除链表的倒数第 N 个结点

直接分情况讨论：list.length=1(n=1), n=list.length, 1<n<list.length

function removeNthFromEnd(head: ListNode | null, n: number): ListNode | null {
    if (!head) {
        return head;
    }

    const nodeList: Array<ListNode> = [];
    let temp = head;
    while (temp) {
        nodeList.push(temp);
        temp = temp.next;
    }

    if (nodeList.length === 1) {
        head = null;
    } else if (n === nodeList.length) {
        head.next = null;
        head = nodeList[1];
    } else {
        if (n === 1) {
            const preNode = nodeList[nodeList.length - n - 1];
            preNode.next = null;
        } else {
            const preNode = nodeList[nodeList.length - n - 1];
            let node: ListNode | null = nodeList[nodeList.length - n];
            const nexNode = nodeList[nodeList.length - n + 1];
            preNode.next = nexNode;
            node.next = null;
            // 释放引用
            node = null;
        }
    }

    // 释放引用
    nodeList.length = 0;
    return head;
}

快慢指针

function removeNthFromEnd(head: ListNode | null, n: number): ListNode | null {
    if (head) {
        let runner = head,
            chaser = head;
        // 快指针先移动n步
        while (n) {
            runner = runner.next;
            n--;
        }
        // 删除头节点
        if (runner === null) return head.next;
        // 移动到尾部
        while (runner.next !== null) {
            runner = runner.next;
            chaser = chaser.next;
        }
        // 删除目标节点
        chaser.next = chaser.next.next;
    }
    return head;
}

11. 有效的括号

栈：

function isValid(s: string): boolean {
    const map = new Map([
            ['(', ')'],
            ['[', ']'],
            ['{', '}']
        ]),
        stack = [];
    for (const c of s) {
        if (stack.length > 0 && map.get(stack[stack.length - 1]) === c) stack.pop();
        else stack.push(c);
    }
    return stack.length === 0;
}

12. 合并两个有序链表

思路：使用一个假节点作为头节点减少了很多判断

function mergeTwoLists(list1: ListNode | null, list2: ListNode | null): ListNode | null {
    if (!list1 || !list2) return list1 ?? list2;
    const head = new ListNode();
    let node = head;
    while (list1 && list2) {
        if (list1.val < list2.val) {
            node.next = list1;
            list1 = list1.next;
        } else {
            node.next = list2;
            list2 = list2.next;
        }
        node = node.next;
    }
    node.next = list1 ?? list2;
    return head.next;
}

13. 括号生成

思路：深度优先遍历(回溯算法)+剪枝

function generateParenthesis(n: number): string[] {
    const res: string[] = [];
    dfs('', n, n, res);
    return res;
}

// buffer -> 当前字符串，left/right -> 左/右括号剩余数量，res -> 结果集
function dfs(buffer: string, left: number, right: number, res: string[]): void {
    // 到达叶子节点
    if (left === 0 && right === 0) {
        res.push(buffer);
        return;
    }

    // 左括号剩余数量严格大于右括号，则字符不是有效的，进行【剪枝】操作
    if (left > right) return;
    // 遍历左右节点
    if (left > 0) dfs(buffer + '(', left - 1, right, res);
    if (right > 0) dfs(buffer + ')', left, right - 1, res);
}

14. 合并 K 个升序链表

思路一：每次循环找到数组中值最小的节点，进行列表拼接(耗时较长)

function mergeKLists(lists: Array<ListNode | null>): ListNode | null {
    let node = new ListNode();
    const head = node;
    while (lists.some((list) => list)) {
        let minNode = new ListNode(1 * 10 ** 4 + 1),
            index = '';
        // 遍历找到最小节点
        for (let i in lists) {
            if (lists[i] && lists[i].val < minNode.val) {
                minNode = lists[i];
                index = i;
            }
        }
        node.next = minNode;
        node = node.next;
        minNode = minNode.next;
        // 替换数组中的元素
        lists[index] = minNode;
    }

    return head.next;
}

思路二：在合并二个列表的基础上合并多个

function mergeKLists(lists: Array<ListNode | null>): ListNode | null {
    let res = null;
    for (const list of lists) {
        res = mergeTwoList(res, list);
    }
    return res;
}

function mergeTwoList(list1: ListNode | null, list2: ListNode | null): ListNode | null {
    if (!list1 || !list2) return list1 ? list1 : list2;
    const head = new ListNode();
    let tail = head;
    while (list1 && list2) {
        if (list1.val < list2.val) {
            tail.next = list1;
            list1 = list1.next;
        } else {
            tail.next = list2;
            list2 = list2.next;
        }
        tail = tail.next;
    }
    tail.next = list1 ? list1 : list2;
    return head.next;
}

思路三：优化思路二，分而治之

function mergeKLists(lists: Array<ListNode | null>): ListNode | null {
    return merge(lists, 0, lists.length - 1);
}

function merge(lists: Array<ListNode | null>, left: number, right: number): ListNode | null {
    if (left === right) return lists[left];
    if (left > right) return null;
    const mid = (left + right) >> 1;
    return mergeTwoList(merge(lists, left, mid), merge(lists, mid + 1, right));
}

function mergeTwoList(list1: ListNode | null, list2: ListNode | null): ListNode | null {
    if (!list1 || !list2) return list1 ?? list2;
    const head = new ListNode();
    let node = head;
    while (list1 && list2) {
        if (list1.val < list2.val) {
            node.next = list1;
            list1 = list1.next;
        } else {
            node.next = list2;
            list2 = list2.next;
        }
        node = node.next;
    }
    node.next = list1 ?? list2;
    return head.next;
}

15. 下一个排列

思路：两遍扫描(比较巧妙，包括倒序数组)，建议查看官方解析：https://leetcode.cn/problems/next-permutation/solution/xia-yi-ge-pai-lie-by-leetcode-solution/

function nextPermutation(nums: number[]): void {
    if (nums.length === 1) return;
    let i = nums.length - 2;
    // 第一遍扫描，找到左边较小的数
    while (i >= 0 && nums[i] >= nums[i + 1]) {
        i--;
    }
    if (i >= 0) {
        let j = nums.length - 1;
        // 第二遍扫描，找到右边较大的数
        while (j > i && nums[j] <= nums[i]) {
            j--;
        }
        swap(nums, i, j);
    }
    reverse(nums, i + 1);
}

// 交换数组中两个元素
function swap(nums: number[], i: number, j: number): void {
    nums[i] = nums[i] ^ nums[j];
    nums[j] = nums[i] ^ nums[j];
    nums[i] = nums[i] ^ nums[j];
}

// 倒序数组末尾
function reverse(nums: number[], start: number): void {
    let i = start,
        j = nums.length - 1;
    while (i < j) {
        swap(nums, i, j);
        i++;
        j--;
    }
}

16. 最长有效括号

思路一：动态规划【时间复杂度 O(n), 空间复杂度 O(n)】

• 记录状态：dp[i]表示以s[i]结尾的有效括号长度
• 确定状态转移方程：dp[i] = 2 + dp[i - 1] + dp[i - dp[i - 1] - 2]

function longestValidParentheses(s: string): number {
    const dp = new Array(s.length).fill(0);
    let max = 0;
    for (let i = 1; i < s.length; i++) {
        if (s.charAt(i) === ')') {
            if (s.charAt(i - 1) === '(') dp[i] = (i > 2 ? dp[i - 2] : 0) + 2;
            else {
                if (i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) === '(') {
                    dp[i] = 2 + dp[i - 1] + (i - dp[i - 1] > 2 ? dp[i - dp[i - 1] - 2] : 0);
                }
            }
        }
        max = Math.max(dp[i], max);
    }
    return max;
}

思路二：栈【时间复杂度 O(n), 空间复杂度 O(n)】

为保持操作一致性，默认在栈中放入-1，表示有效子串是从 0 开始的（巧妙）

function longestValidParentheses(s: string): number {
    const stack = [-1];
    let max = 0;
    for (let i = 0; i < s.length; i++) {
        if (s.charAt(i) === '(') stack.push(i);
        else {
            stack.pop();
            if (stack.length === 0) stack.push(i);
            else max = Math.max(i - stack[stack.length - 1], max);
        }
    }
    return max;
}

思路三：正反向遍历(时间复杂度 O(n), 空间复杂度 O(1))（巧妙）

function longestValidParentheses(s: string): number {
    let l = 0,
        r = 0,
        max = 0;
    // 正向遍历
    for (let i = 0; i < s.length; i++) {
        s.charAt(i) === '(' ? l++ : r++;
        if (l === r) max = Math.max(2 * l, max);
        else if (r > l) l = r = 0;
    }
    l = r = 0;
    // 反向遍历
    for (let j = s.length - 1; j >= 0; j--) {
        s.charAt(j) === '(' ? l++ : r++;
        if (l === r) max = Math.max(2 * l, max);
        else if (l > r) l = r = 0;
    }
    return max;
}

17. 搜索旋转排序数组

类别：二分搜索变种

复杂度：时间复杂度 O(log n)，空间复杂度 O(1)

function search(nums: number[], target: number): number {
    if (nums.length <= 1) return nums.length > 0 && nums[0] === target ? 0 : -1;
    let l = 0,
        r = nums.length - 1,
        mid = 0;
    while (l <= r) {
        mid = (l + r) >> 1;
        if (nums[mid] === target) return mid;
        if (nums[l] <= nums[mid]) {
            // 左半部分有序
            if (nums[l] <= target && target < nums[mid]) r = mid - 1;
            else l = mid + 1;
        } else {
            // 右半部分有序
            if (nums[mid] < target && target <= nums[r]) l = mid + 1;
            else r = mid - 1;
        }
    }
    return -1;
}

18. 在排序数组中查找元素的第一个和最后一个位置

类别：二分搜索变种

复杂度：时间复杂度 O(log n)，空间复杂度 O(1)

function searchRange(nums: number[], target: number): number[] {
    if (nums.length === 0) return [-1, -1];
    const first = searchFirst(nums, target);
    if (first === -1) return [-1, -1];
    const last = searchLast(nums, target);
    return [first, last];
}

function searchFirst(nums: number[], target: number): number {
    let left = 0,
        right = nums.length - 1;
    while (left < right) {
        const mid = (left + right) >> 1;
        if (nums[mid] < target) left = mid + 1;
        else if (nums[mid] === target) right = mid;
        else right = mid - 1;
    }
    return nums[left] === target ? left : -1;
}

function searchLast(nums: number[], target: number): number {
    let left = 0,
        right = nums.length - 1;
    while (left < right) {
        const mid = (left + right + 1) >> 1;
        if (nums[mid] < target) left = mid + 1;
        else if (nums[mid] === target) left = mid;
        else right = mid - 1;
    }
    return nums[left] === target ? left : -1;
}

19. 组合总和

思路：回溯算法，去重思路比较新颖

复杂度：不是很能理解，详细见官方题解：https://leetcode.cn/problems/combination-sum/solution/zu-he-zong-he-by-leetcode-solution/

function combinationSum(candidates: number[], target: number): number[][] {
    let res: number[][] = [];
    // 定义搜索回溯函数
    const dfs = (combine: number[], target: number, idx: number): void => {
        if (idx === candidates.length) return; // 最大深度
        if (target === 0) {
            // 找到结果集
            res.push(combine);
            return;
        }
        // 跳过当前节点
        dfs(combine, target, idx + 1);
        // 使用当前节点
        if (target - candidates[idx] >= 0)
            dfs([...combine, candidates[idx]], target - candidates[idx], idx);
    };
    dfs([], target, 0);
    return res;
}

20. 接雨水

思路一：直观解决

复杂度：时间复杂度 O(n^2^)，空间复杂度 O(1)

核心思想：每个位置接的雨水单位等于Math.min(left_max, right_max) - heights[cur]，其中left_max、right_max分别表示从开始位置到当前位置的最大值、从当前位置到结束位置的最大值

function trap(heights: number[]): number {
    let ans = 0,
        left_max = 0,
        right_max = 0;
    for (let i = 0; i < heights.length; i++) {
        for (let j = 0; j <= i; j++) {
            if (heights[j] > left_max) left_max = heights[j];
        }
        for (let j = i; j < heights.length; j++) {
            if (heights[j] > right_max) right_max = heights[j];
        }
        ans += Math.min(left_max, right_max) - heights[i];
        (left_max = 0), (right_max = 0);
    }
    return ans;
}

思路二：动态规划

复杂度：时间复杂度 O(n)，空间复杂度 O(n)

核心思想：在思路一的基础上，提前存储从左往右每个位置左边高度的最大值和从右往左每个位置右边高度的最大值，最后进行一次遍历，得到结果

function trap(heights: number[]): number {
    if (heights.length < 3) return 0;
    const len = heights.length,
        left_max_arr: number[] = [],
        right_max_arr: number[] = [];
    let ans = 0;
    (left_max_arr[0] = heights[0]), (right_max_arr[len - 1] = heights[len - 1]);
    for (let i = 1; i < len; i++) {
        left_max_arr[i] = Math.max(heights[i], left_max_arr[i - 1]);
    }
    for (let j = len - 2; j > -1; j--) {
        right_max_arr[j] = Math.max(heights[j], right_max_arr[j + 1]);
    }
    for (let i = 0; i < len - 1; i++) {
        ans += Math.min(left_max_arr[i], right_max_arr[i]) - heights[i];
    }
    return ans;
}

思路三：单调递减栈

复杂度：时间复杂度 O(n)，空间复杂度 O(n)

核心思想：积水处只能在低洼处形成，当后面的柱子高度比前面的低时，是无法接雨水的（后面的柱子可能储水）。所以使用单调递减栈存储可能储水的柱子，当找到一根比前面高的柱子，就可以计算接到的雨水

function trap(heights: number[]): number {
    let ans = 0,
        i = 0,
        lastIdx = 0;
    const stack: number[] = []; // 单调递减栈
    while (i < heights.length) {
        lastIdx = stack.length - 1;
        while (stack.length > 0 && heights[i] >= heights[stack[lastIdx]]) {
            const top = stack.pop();
            if (stack.length === 0) break; // 柱子高度递增，不可能形成水洼
            lastIdx = stack.length - 1;
            const w = i - stack[lastIdx] - 1; // 形成水洼的宽度
            const h = Math.min(heights[stack[lastIdx]], heights[i]) - heights[top as number]; // 形成水洼的高度
            ans += w * h;
        }
        stack.push(i++); // 后续柱子可能与当前柱子形成水洼
    }
    return ans;
}

思路四：双指针

复杂度：时间复杂度 O(n)，空间复杂度 O(1)

核心思想：在动态规划的基础上，使用双指针和两个变量(leftMax、rightMax)替换 O(n)的存储空间，很巧妙

function trap(heights: number[]): number {
    let ans = 0,
        left = 0,
        leftMax = 0,
        right = heights.length - 1,
        rightMax = 0;
    while (left < right) {
        leftMax = Math.max(heights[left], leftMax);
        rightMax = Math.max(heights[right], rightMax);
        if (heights[left] < heights[right]) {
            // 此时必有leftMax<rightMax（注意过程）
            // 因为leftMax和rightMax分别由heights[left]、heights[right]逐渐产生的
            // 拿到leftMax后就可以计算当前位置的水洼积水量
            // 因为当前位置的积水量是由当前位置leftMax、rightMax最小值决定的
            ans += leftMax - heights[left];
            left++;
        } else {
            // 反之同理，leftMax>=rightMax
            // 通过片段，即可求得当前位置的积水量
            ans += rightMax - heights[right];
            right--;
        }
    }
    return ans;
}

21. 全排列

思路：回溯算法

复杂度：时间复杂度 O(n _ n!)，空间复杂度 O(n _ n!)，n 为数组的长度

核心思想：每一个节点表示了求解问题的不同阶段，深度优先遍历在回到上一层节点时，需要“状态重置”，状态变量如下：

• 已经选了哪些数：path
• 使用的布尔数组：used

function permute(nums: number[]): number[][] {
    const ans: number[][] = [],
        used: boolean[] = new Array(nums.length);
    used.fill(false);
    dfs(nums, [], used, ans);
    return ans;
}

function dfs(nums: number[], path: number[], used: boolean[], ans: number[][]): void {
    if (path.length === nums.length) {
        ans.push([...path]);
        return;
    }
    for (let i = 0; i < nums.length; i++) {
        if (used[i]) continue;
        path.push(nums[i]);
        used[i] = true;
        dfs(nums, path, used, ans);
        path.pop();
        used[i] = false;
    }
}

22. 旋转图像

思路一：使用辅助数组

复杂度：时间复杂度 O(n^2^)，空间复杂度 O(n^2^)

核心思想：matrix[row][col] => matrix_new[col][n - row - 1]

/**
 Do not return anything, modify matrix in-place instead.
 */
function rotate(matrix: number[][]): void {
    const n = matrix.length;
    const matrix_new = new Array(n).fill(0).map((_) => new Array(n).fill(0));
    for (let i = 0; i < n; i++) {
        for (let j = 0; j < n; j++) {
            matrix_new[j][n - i - 1] = matrix[i][j];
        }
    }
    for (let i = 0; i < n; i++) {
        for (let j = 0; j < n; j++) {
            matrix[i][j] = matrix_new[i][j];
        }
    }
}

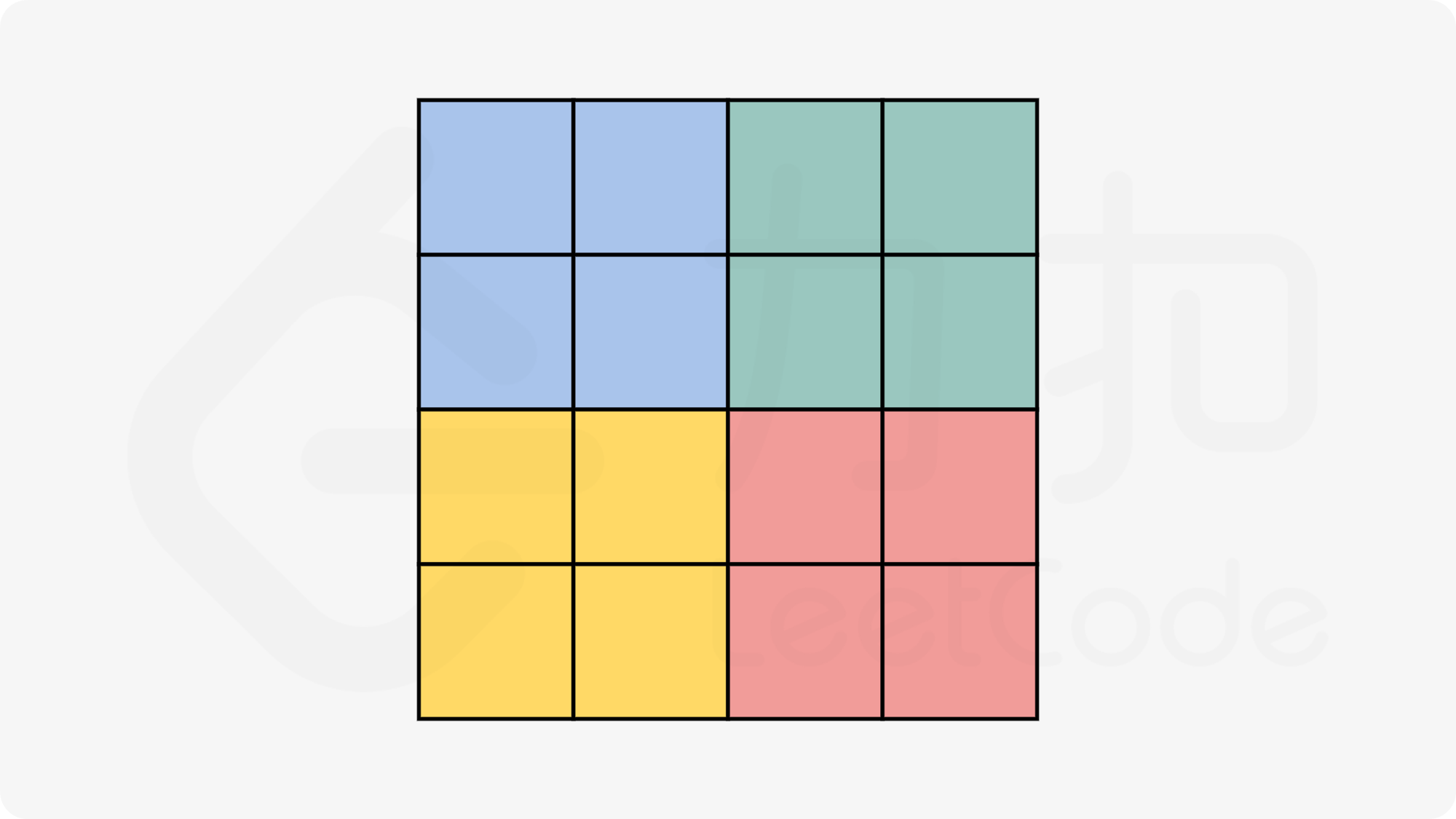
思路二：原地旋转

复杂度：时间复杂度 O(n^2^)，空间复杂度 O(1)

核心思想：确定旋转区域，每次旋转该区域对应的其它区域上的总共 4 个元素

/**
 Do not return anything, modify matrix in-place instead.
 */
function rotate(matrix: number[][]): void {
    const n = matrix.length;
    for (let i = 0; i < Math.floor(n / 2); i++) {
        for (let j = 0; j < Math.floor((n + 1) / 2); j++) {
            const temp = matrix[i][j];
            matrix[i][j] = matrix[n - j - 1][i];
            matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
            matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
            matrix[j][n - i - 1] = temp;
        }
    }
}

思路三：用翻转代替旋转

复杂度：时间复杂度 O(n^2^)，空间复杂度 O(1)

核心思想：先通过水平翻转（matrix[i][j] => matrix[n - i - 1][j]，再通过对角线翻转（matrix[i][j] => matrix[j][i]），最终得到的结果和上述两种思路是一致的，即matrix[i][j] => matrix[j][n - i - 1]

/**
 Do not return anything, modify matrix in-place instead.
 */
function rotate(matrix: number[][]): void {
    const n = matrix.length;
    // 水平翻转
    for (let i = 0; i < Math.floor(n / 2); i++) {
        for (let j = 0; j < n; j++) {
            [matrix[i][j], matrix[n - i - 1][j]] = [matrix[n - i - 1][j], matrix[i][j]];
        }
    }
    // 主对角线翻转
    for (let i = 0; i < n; i++) {
        for (let j = 0; j < i; j++) {
            [matrix[i][j], matrix[j][i]] = [matrix[j][i], matrix[i][j]];
        }
    }
}

通过解构赋值交换两数，效率较低，通过异或交换两数相对更快

/**
 Do not return anything, modify matrix in-place instead.
 */
function rotate(matrix: number[][]): void {
    const n = matrix.length;
    // 水平翻转
    for (let i = 0; i < Math.floor(n / 2); i++) {
        for (let j = 0; j < n; j++) {
            matrix[i][j] = matrix[i][j] ^ matrix[n - i - 1][j];
            matrix[n - i - 1][j] = matrix[i][j] ^ matrix[n - i - 1][j];
            matrix[i][j] = matrix[i][j] ^ matrix[n - i - 1][j];
        }
    }
    // 主对角线翻转
    for (let i = 0; i < n; i++) {
        for (let j = 0; j < i; j++) {
            matrix[i][j] = matrix[i][j] ^ matrix[j][i];
            matrix[j][i] = matrix[i][j] ^ matrix[j][i];
            matrix[i][j] = matrix[i][j] ^ matrix[j][i];
        }
    }
}

23. 字母异位词分组

思路：使用 Map 结构

复杂度：时间复杂度 O(n)，空间复杂度 O(n)（不计算生成有序字符串）

function groupAnagrams(strs: string[]): string[][] {
    const map: Map<string, string[]> = new Map();
    for (const str of strs) {
        const sortedStr = str.split('').sort().join('');
        if (map.has(sortedStr)) map.get(sortedStr)?.push(str);
        else map.set(sortedStr, [str]);
    }
    return Array.from(map.values());
}

24. 最大子数组和

思路一：贪心算法

复杂度：时间复杂度 O(n)，空间复杂度 O(1)

核心思想：若当前指针所指元素之前的和小于 0，则丢弃当前元素之前的数列

注意：该题只需要求出最大子数组和，不需要知道子数组是什么

function maxSubArray(nums: number[]): number {
    let cur = nums[0],
        max = nums[0];
    for (let i = 1; i < nums.length; i++) {
        cur = Math.max(nums[i], nums[i] + cur);
        max = Math.max(cur, max);
    }
    return max;
}

思路二：动态规划

复杂度：时间复杂度 O(n)，空间复杂度 O(1)

核心思想：若前一个元素大于 0，则将其加到当前元素上

function maxSubArray(nums: number[]): number {
    for (let i = 1; i < nums.length; i++) {
        if (nums[i - 1] > 0) nums[i] += nums[i - 1];
    }
    return Math.max(...nums);
}

25. 跳跃游戏

思路一：回溯算法

function canJump(nums: number[]): boolean {
    const res: boolean[] = []; // 是否走到终点
    dfs(nums, 0, res);
    return res.includes(true);
}

function dfs(nums: number[], idx: number, res: boolean[]) {
    if (idx === nums.length - 1) return res.push(true); // 走到终点
    if (nums[idx] === 0) return; // 无法走到终点
    for (let i = 1; i <= nums[idx]; i++) {
        if (res.includes(true)) return; // 已走到终点，不用进行后续操作
        dfs(nums, idx + i, res);
    }
}

遇到复杂的测试案例，会超时

方法二：可以到达的最远位置

复杂度：时间复杂度 O(n)，空间复杂度 O(1)

核心思想：用变量记录可以到达的最远位置，详情如下：

function canJump(nums: number[]): boolean {
    let reach = 0;
    for (let i = 0; i < nums.length; i++) {
        if (i > reach) return false;
        reach = Math.max(i + nums[i], reach);
    }
    return true;
}

方法三：最早开始的位置

复杂度：时间复杂度 O(n)，空间复杂度 O(1)

核心思想：从后往前进行遍历，找到最早开始的位置

function canJump(nums: number[]): boolean {
    let last = nums.length - 1;
    for (let i = nums.length - 2; i > -1; i--) {
        if (i + nums[i] >= last) last = i;
    }
    return last === 0;
}

26. 合并区间

思路：排序 + 合并处理

复杂度：时间复杂度 O(n)，空间复杂度 O(n)==不考虑排序算法的复杂度==

核心思想：首先，按照区间开头进行排序，然后从前往后直接处理

function merge(intervals: number[][]): number[][] {
    intervals.sort((a, b) => a[0] - b[0]);
    const ans: number[][] = [intervals[0]];
    for (let i = 1; i < intervals.length; i++) {
        if (ans[ans.length - 1][1] >= intervals[i][0]) {
            // 需要进行合并
            ans[ans.length - 1][1] = Math.max(intervals[i][1], ans[ans.length - 1][1]);
        } else ans.push(intervals[i]);
    }
    return ans;
}

27. 不同路径

思路一：排列组合

复杂度：时间复杂度 O(n)，空间复杂度 O(1)

核心思想：在m × n的网格中，机器人左要走n - 1步，向下要走m - 1步，实际结果就是计算组合：$C^{m-1}_{m+n-2}=\frac{(m+n-2)!}{(m-1)!·(n-1)!}$

function uniquePaths(m: number, n: number): number {
    return factorial(m + n - 2) / (factorial(m - 1) * factorial(n - 1));
}

// 计算n!
function factorial(n: number): number {
    let ans = 1;
    for (let i = 2; i <= n; i++) {
        ans *= i;
    }
    return ans;
}

思路二：动态规划

复杂度：时间复杂度 O(mn)，空间复杂度 O(mn)

核心思想：dp[i][j] = dp[i-1][j] + dp[i][j-1]

function uniquePaths(m: number, n: number): number {
    const dp: number[][] = new Array(m).fill(0).map((_) => new Array(n).fill(0));
    for (let i = 0; i < m; i++) {
        dp[i][0] = 1;
    }
    for (let j = 0; j < n; j++) {
        dp[0][j] = 1;
    }
    for (let i = 1; i < m; i++) {
        for (let j = 1; j < n; j++) {
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        }
    }
    return dp[m - 1][n - 1];
}

28. 最小路径和

思路：动态规划

复杂度：时间复杂度 O(mn)，空间复杂度 O(1)

核心思想：dp[i][j] = dp[i-1][j] + dp[i][j-1]，注意初始化时dp[i][0]、dp[0][j]需要迭代状态

function minPathSum(grid: number[][]): number {
    const m = grid.length,
        n = grid[0].length;
    for (let i = 1; i < m; i++) {
        grid[i][0] += grid[i - 1][0];
    }
    for (let j = 1; j < n; j++) {
        grid[0][j] += grid[0][j - 1];
    }
    for (let i = 1; i < m; i++) {
        for (let j = 1; j < n; j++) {
            grid[i][j] += Math.min(grid[i - 1][j], grid[i][j - 1]);
        }
    }
    return grid[m - 1][n - 1];
}

29. 爬楼梯

思路一：动态规划

复杂度：时间复杂度 O(n)，空间复杂度 O(n)==可以使用变量存储降低空间复杂度为 O(1)==

核心思想：dp[i] = dp[i - 1] + dp[i - 2]

function climbStairs(n: number): number {
    if (n < 3) return n;
    const dp = new Array(n).fill(0);
    (dp[0] = 1), (dp[1] = 2);
    for (let i = 2; i < n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[n - 1];
}

思路二：递归

数值过大，会导致超时

function climbStairs(n: number): number {
    if (n < 3) return n;
    return climbStairs(n - 1) + climbStairs(n - 2);
}

30. 编辑距离

==本题核心是找到子问题==

思路一：递归

核心思想：从最后一位进行判断，转换为自顶向下的递归问题

function minDistance(word1: string, word2: string): number {
    if (word1.length === 0 || word2.length === 0) {
        return Math.max(word1.length, word2.length); // 执行删除或插入操作
    }
    if (word1.charAt(word1.length - 1) === word2.charAt(word2.length - 1)) {
        // 无需进行额外操作
        return minDistance(word1.slice(0, word1.length - 1), word2.slice(0, word2.length - 1));
    }
    return (
        Math.min(
            minDistance(word1, word2.slice(0, word2.length - 1)), // 执行插入操作
            minDistance(word1.slice(0, word1.length - 1), word2), // 执行删除操作
            minDistance(word1.slice(0, word1.length - 1), word2.slice(0, word2.length - 1)) // 执行替换操作
        ) + 1
    );
}

对于复杂的单词会超时

思路二：动态规划

复杂度：时间复杂度 O(mn)，空间复杂度 O(mn)（m、n 分别为 word1、word2 的长度）

核心思想：

• 确定状态：dp[i][j]表示 word1 长度为 i，word2 长度为 j 的最小操作次数
• 推导状态转移方程：
  • 如果word1[i] === word2[j]，那么dp[i][j] = dp[i-1][j-1]
  • 否则，dp[i][j] = 1 + min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1])

function minDistance(word1: string, word2: string): number {
    const m = word1.length,
        n = word2.length;
    const dp: number[][] = new Array(m + 1).fill(0).map((_) => new Array(n + 1).fill(0));
    for (let i = 0; i <= m; i++) {
        dp[i][0] = i;
    }
    for (let j = 0; j <= n; j++) {
        dp[0][j] = j;
    }
    for (let i = 1; i <= m; i++) {
        for (let j = 1; j <= n; j++) {
            if (word1.charAt(i - 1) === word2.charAt(j - 1)) dp[i][j] = dp[i - 1][j - 1];
            else dp[i][j] = 1 + Math.min(dp[i][j - 1], dp[i - 1][j], dp[i - 1][j - 1]);
        }
    }
    return dp[m][n];
}

31. 颜色分类（”荷兰国旗问题“）

思路一：使用快速排序 partition 的思想

复杂度：时间复杂度 O(n)，空间复杂度 O(1)

核心思想：见基础->排序->快速排序

/**
 Do not return anything, modify nums in-place instead.
 */
function sortColors(nums: number[]): void {
    let index = 0;
    for (let i = index; i < nums.length; i++) {
        if (nums[i] < 1) swap(nums, i, index++);
    }
    index = nums.length - 1;
    for (let j = index; j > -1 && nums[j] !== 0; j--) {
        if (nums[j] > 1) swap(nums, j, index--);
    }
}

function swap(nums: number[], i: number, j: number): void {
    const temp = nums[i];
    nums[i] = nums[j];
    nums[j] = temp;
}

思路二：双指针（p0，p1）

复杂度：时间复杂度 O(n)，空间复杂度 O(1)

核心思想：用p0、p1来记录开头可存储的位置，和思路一类似，注意特殊情况

function sortColors(nums: number[]): void {
    let p0 = 0,
        p1 = 0;
    for (let i = 0; i < nums.length; i++) {
        if (nums[i] === 1) swap(nums, i, p1++);
        else if (nums[i] === 0) {
            swap(nums, i, p0);
            if (p0 < p1) swap(nums, i, p1);
            p0++;
            p1++;
        }
    }
}

function swap(nums: number[], i: number, j: number): void {
    const temp = nums[i];
    nums[i] = nums[j];
    nums[j] = temp;
}

思路三：双指针（p0，p2）

复杂度：时间复杂度 O(n)，空间复杂度 O(1)

核心思想：思想和思路二类似，需要注意的是交换p2得到的新nums[i]值仍然可能是 2，需要不断进行交换，直到nums[i]不是 2

function sortColors(nums: number[]): void {
    let p0 = 0,
        p2 = nums.length - 1;
    for (let i = 0; i <= p2; i++) {
        while (i <= p2 && nums[i] === 2) swap(nums, i, p2--);
        if (nums[i] === 0) swap(nums, i, p0++);
    }
}

function swap(nums: number[], i: number, j: number): void {
    const temp = nums[i];
    nums[i] = nums[j];
    nums[j] = temp;
}

32. 最小覆盖子串

思路：滑动窗口

核心思想：用两个Map存储信息：第一个统计 t 字符串字符种类和数目，第二个统计遍历过程中 s 字符串字符种类和数目，当窗口覆盖子串时记录信息，缩小窗口，直到 s 字符串遍历完成

function minWindow(s: string, t: string): string {
    const ori: Map<string, number> = new Map(); // 统计t中原有字符的种类和个数
    const cnt: Map<string, number> = new Map(); // 遍历s过程中，统计字符的种类和个数
    for (const c of t) {
        ori.set(c, (ori.get(c) ?? 0) + 1);
    }
    let l = 0,
        r = -1,
        ansL = -1,
        ansR = -1,
        len = Number.MAX_SAFE_INTEGER;
    while (r < s.length) {
        r++;
        cnt.set(s[r], (cnt.get(s[r]) ?? 0) + 1);
        while (check(ori, cnt) && l <= r) {
            if (r - l + 1 < len) {
                len = r - l + 1;
                ansL = l;
                ansR = l + len;
            }
            if (cnt.has(s[l])) cnt.set(s[l], (cnt.get(s[l]) ?? 0) - 1);
            l++;
        }
    }
    return ansL === -1 ? '' : s.slice(ansL, ansR);
}

// 检测滑动窗口中的字符是否涵盖t
function check(ori: Map<string, number>, cnt: Map<string, number>): boolean {
    for (const [c, count] of ori.entries()) {
        if ((cnt.get(c) ?? 0) < count) return false;
    }
    return true;
}

33. 子集

思路一：回溯算法（使用used数组）

复杂度：略

核心思想：使用used数组进行回溯，筛选条件见代码

function subsets(nums: number[]): number[][] {
    const ans: number[][] = [],
        used = new Array(nums.length).fill(false);
    dfs(nums, ans, used, []);
    return ans;
}

function dfs(nums: number[], ans: number[][], used: boolean[], buffer: number[]) {
    ans.push([...buffer]);
    for (let i = 0; i < nums.length; i++) {
        if (used[i] || (buffer.length > 0 && buffer[buffer.length - 1] > nums[i])) continue;
        buffer.push(nums[i]);
        used[i] = true;
        dfs(nums, ans, used, buffer);
        buffer.pop();
        used[i] = false;
    }
}

思路二：回溯算法（不使用used数组）

复杂度：略

核心思想：求子集比较特殊，从前往后直接遍历就可以了

function subsets(nums: number[]): number[][] {
    const ans: number[][] = [];
    dfs(nums, ans, [], 0);
    return ans;
}

function dfs(nums: number[], ans: number[][], buffer: number[], begin: number) {
    ans.push([...buffer]);
    for (let i = begin; i < nums.length; i++) {
        buffer.push(nums[i]);
        dfs(nums, ans, buffer, i + 1);
        buffer.pop();
    }
}

34. 单词搜索

思路：回溯算法

复杂度：略

核心思想：定义check(i, j, k)函数，判断board[i][j]处开始是否能找到字符串word[k...]，最终结果是遍历board每个元素开始是否能找到word，详细请见题解

function exist(board: string[][], word: string): boolean {
    const w = board[0].length,
        h = board.length;
    const used: boolean[][] = new Array(h).fill(0).map((_) => new Array(w).fill(false));
    const directions = [
        [-1, 0],
        [0, 1],
        [1, 0],
        [0, -1]
    ]; // 方式不错，值得借鉴
    const check = (i: number, j: number, k: number): boolean => {
        if (board[i][j] !== word[k]) return false;
        if (k === word.length - 1) return true;
        let res = false;
        used[i][j] = true;
        for (const [dx, dy] of directions) {
            const newX = i + dx,
                newY = j + dy; // 方式不错，值得借鉴
            if (newX > -1 && newX < h && newY > -1 && newY < w && !used[newX][newY]) {
                res = check(newX, newY, k + 1);
                if (res) break;
            }
        }
        used[i][j] = false;
        return res;
    };
    for (let i = 0; i < h; i++) {
        for (let j = 0; j < w; j++) {
            if (check(i, j, 0)) return true;
        }
    }
    return false;
}

35. 柱状图中最大的矩形